Understanding Projectile Motion: How Velocity, Angle, and Height Shape the Trajectory
Projectile motion is one of the most fascinating topics in physics, combining intuition, mathematics, and real-world applications. Whether it’s a soccer ball soaring into a goal, a cannonball launched from a fort, or a basketball arcing toward the hoop, understanding projectile motion allows us to predict how objects travel through space under the influence of gravity.
In this article, we’ll break down the core concepts, explore the impact of key parameters, and see how to calculate the range, maximum height, and time of flight of a projectile.
Tip: You can also simulate various projectile motions using the Launch button shown at the top of this page to see how changing the velocity, angle, or height affects the trajectory in real time.
What is Projectile Motion?
Projectile motion refers to the motion of an object that is thrown, launched, or projected into the air and moves under the influence of gravity alone (assuming air resistance is negligible). This motion is two-dimensional, meaning it has both horizontal and vertical components:
- Horizontal motion: constant velocity, because there is no acceleration in the horizontal direction (ignoring air resistance).
- Vertical motion: accelerated motion due to gravity, pulling the object downward at 9.8 m/s².
The combination of these two motions produces a curved trajectory, typically a parabola.
Key Parameters Affecting Projectile Motion
1. Initial Velocity (v₀)
The initial velocity is the speed at which the projectile is launched. It can be broken into horizontal (vₓ) and vertical (vᵧ) components:
Horizontal velocity: vₓ = v₀ × cos(θ) Vertical velocity: vᵧ = v₀ × sin(θ)
where θ is the launch angle relative to the horizontal.
Impact:
- Higher v₀ increases both the range and maximum height.
- Faster projectiles stay in the air longer if the vertical component is larger.
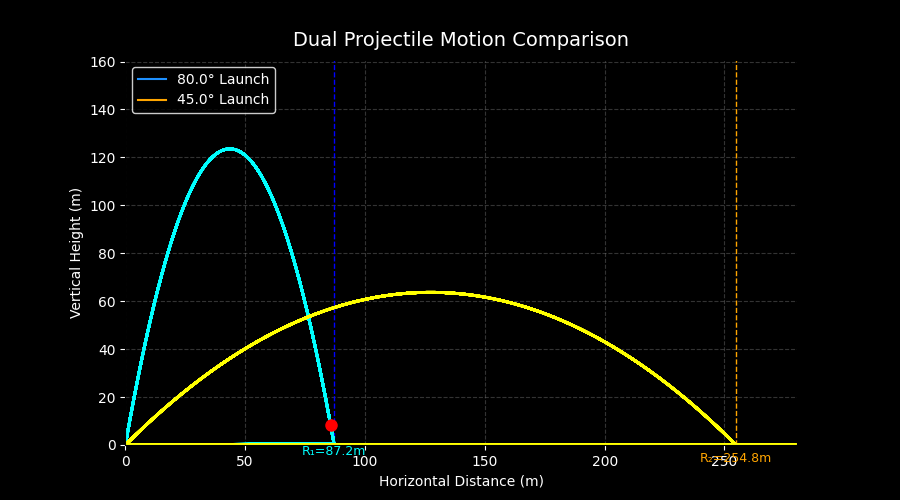
2. Launch Angle (θ)
The angle of projection determines how the initial velocity is split between horizontal and vertical motion.
Key points:
- 45°: Produces the maximum horizontal range on level ground.
- < 45°: Lower range but quicker time of flight.
- > 45°: Higher maximum height, longer time of flight, but shorter range.
3. Initial Height (h₀)
If the projectile is launched from a height above the ground (e.g., a cliff or a building), it can stay in the air longer and cover more distance.
Impact:
- Higher initial height increases time of flight and can increase the range depending on the launch angle.
- Maximum height is also naturally higher by the initial height.
Calculating Key Quantities
1. Time of Flight (T)
The total time the projectile spends in the air. For a projectile launched from height h₀:
T = (v₀ × sin(θ) + sqrt((v₀ × sin(θ))² + 2 × g × h₀)) / g
If launched from ground level (h₀ = 0):
T = 2 × v₀ × sin(θ) / g
2. Maximum Height (H)
The peak of the projectile’s trajectory:
H = h₀ + (v₀ × sin(θ))² / (2 × g)
3. Range (R)
The horizontal distance traveled before hitting the ground:
R = v₀ × cos(θ) × T
For level ground (h₀ = 0):
R = (v₀² × sin(2 × θ)) / g
Note: Range is maximum when θ = 45°.
How Parameters Affect Motion Visually
| Parameter | Effect on Trajectory |
|---|---|
| Initial velocity v₀ | Higher speed → longer range & higher peak |
| Launch angle θ | Low angle → flat & fast; high angle → tall & slow; 45° → longest range |
| Initial height h₀ | More height → longer flight & distance, higher apex |
Summary
Projectile motion is an elegant combination of horizontal uniform motion and vertical free fall. By adjusting initial velocity, launch angle, and initial height, we can control how far, how high, and how long a projectile travels.
With the formulas for time of flight, maximum height, and range, you can predict a projectile’s trajectory accurately — making physics not just theoretical, but practical and fun!
Tip: Don’t forget to try the Launch button at the top to simulate different projectiles in real time and see how changing parameters affects the motion.
